Notes of Uri Bader IHES lectures october 5th, 2021

Algebraic representations of ergodic actions

Based on joint work with Alex Furman, and earlier litterature.

Thanks to Sami Douba for his help with notetaking.

Today, we start with basics on measure spaces and algebraic varieties. Later on, we shall merge both subjects together.

1. Ergodic theory of algebraic varieties

1.1. Algebraic actions

${k}$ is a local field. For simplicity, characteristic is ${0}$ but most of what I will say extends to positive characteristic. Also to nonlocal complete normed fields. ${\mathbb{G}}$ is an algebraic group acting algebraically on an algebraic variety ${\mathbb{V}}$ . Then ${G=\mathbb{G}(k)}$ acts on ${V=\mathbb{V}(k)}$ . We equip ${V}$ with the ${k}$ -topology, it is second countable and locally compact.

Questions. What can one say of the structure of orbits?

Examples. ${SL_2({\mathbb R})}$ acting on ${{\mathbb R}^2}$ has ${2}$ orbits, one open and one closed. Let ${K=SO(2)}$ , ${P=}$ triangular matrices, ${A=}$ diagonal matrices, ${U=}$ unipotent matrices. Then ${K}$ -orbits are concentric circles, ${P}$ -orbits are the origin, two halflines and two halfplanes. ${A}$ -orbits are the origin, four halflines and branches of hyperbolas. ${U}$ -orbits are points of the ${s}$ -axis and two halplanes.

We observe that orbits are open or closed, except for halflines which are nearly closed: intersections of an open and a closed set. We call such sets locally closed

Fact: Orbits of algebraic actions are locally closed.

Consequences.

${G}$ -invariant open sets separate points in distinct orbit in ${V}$ . It follows that the quotient topology on ${V/G}$ is second countable and ${T_0}$ (topology separates points). This is known as Chevalley Theorem (combined with a result of Borel-Serre).

The Borel structure on ${V/G}$ is countably separated. It follows that there exists a Borel embedding of ${V/G}$ to ${[0,1]}$ .

A fundamental theorem of Descriptive Set Theory states that all uncountable Polish topological spaces (completely metrizable, admitting a countable dense subset) are isomorphic as Borel spaces. See Kechris’ book. Such Borel spaces are called standard Borel spaces.

Examples. Finite sets, countable sets, ${[0,1]\simeq\{ 0,1 \}^{\mathbb N}\simeq}$ a separable Hilbert space.

A Borel space is said to be countably separated if there exists a countable collection of Borel sets that separates points (equivalently, space has a Borel embedding into ${\{ 0,1 \}^{\mathbb N}}$ ). Standard Borel sets have this property.

We take this encouraging fact as an invitation to do ergodic theory.

1.2. measures and measure classes

Say two measures on a Borel space are equivalent if they have the same sigma-ideal of null sets. A measure class could be understood as the choice of a sigma-ideal.

Warning. Not every sigma-ideal comes from a measure. For instance, the sigma-ideal of meager sets does not arise from a measure.

Examples.

${V}$ has a natural volume measure class.

${G}$ has the Haar measure class.

For every closed subgroup ${S<G}$ , ${G/S}$ has a unique ${G}$ -invariant measure class, called the Haar class. Warning: very rarely does ${G/S}$ admit a ${G}$ -invariant measure. For instance, ${SL_n(k)}$ acting on projective space ${P^{n-1}(k)}$ has no invariant measure in the Haar class. More generally, when ${G}$ is simple and ${Q}$ is parabolic, ${G/Q}$ has no invariant measure in the Haar class.

If ${S}$ is a locally compact group, Haar measure is finite iff ${S}$ is compact. If ${T<S}$ is a closed normal subgroup, then ${S/T}$ has a finite invariant measure iff ${T}$ is cocompact in ${S}$ .

Definition 1 Say that a ${G}$ -invariant measure class on ${V}$ is ergodic if every ${G}$ -invariant Borel set is either null or full (complement is null).

Equivalently, every a.e. defined Borel ${G}$ -invariant map ${V\rightarrow[0,1]}$ is a.e. constant. Here, ${[0,1]}$ can be replaced with any countably separated space.

Corollary 2 Every ${G}$ -ergodic measure class on ${V}$ is supported on a single orbit. Moreover, it coincides with the Haar class on this orbit.

Indeed, think of the action as a ${G}$ -map ${X\rightarrow V}$ where ${X}$ is a ${G}$ -ergodic space. Since ${V/G}$ is countably separated, this map must be a.e. constant. This leads to a map ${X\rightarrow G/H}$ to an orbit. This must be a Borel and measure class isomorphism, thanks to the uniqueness of the Haar class.

In the nonergodic case, one can use ergodic decompositions.

Definition 3 Given a ${G}$ -measure class ${[\nu]}$ on ${V}$ , since ${V/G}$ is countably separated, for every measure ${\nu}$ in the class, there exists a family of ${G}$ -invariant measures ${t\mapsto \nu_t}$ on ${V}$ , ${t\in V/G}$ , such that ${\nu_t}$ is a Haar measure on the orbit denoted by ${t}$ , and

$\displaystyle \nu=\int_{V/G} \nu_t d\bar{\nu}(t).$

This is the ergodic decomposition of ${[\nu]}$ .

In particular, the measure class ${[\nu]}$ is fully determined by the class of the pushed-forward measure ${[\bar{\nu}]}$ .

1.3. Classification of ${G}$ -invariant probability measures

If ${N<G}$ is a normal ${k}$ -algebraic subgroup, which is cocompact, then ${G/N}$ has a finite Haar measure. By Noetherianity, there exists a minimal element ${N_0}$ among such cocompact normal ${k}$ -algebraic subgroups. In fact, ${N_0}$ is a least element. Indeed, given ${N}$ and ${N'}$ , ${G/(N\cap N')}$ maps to a closed subset of ${(G/N)\times(G/N')}$ hence is compact.

Theorem 4 If ${G}$ has no compact factors (i.e. ${N_0=G}$ ), then every ${G}$ -invariant probability measure on ${V}$ is supported on fixed points.
In general, every ${G}$ -invariant probability measure on ${V}$ is supported on the ${N_0}$ -fixed points.

Example. For ${G=SL_2({\mathbb R})}$ acting on ${{\mathbb R}^2}$ , the only ${G}$ -invariant probability measure is the Dirac mass at the origin. Same picture for ${P}$ , ${A}$ and ${U}$ (with as many invariant measures as there are measure on the ${x}$ -axis). However, ${K=SO(2)}$ has a lot of invariant measures.

This implies Borel’s density theorem.

Theorem 5 (Borel) If has no compact factor, and ${\Gamma<G}$ is a lattice, then ${\Gamma}$ is Zariski-dense in ${G}$ .

Indeed, let ${Z}$ be the Zariski closure of ${\Gamma}$ , then push the ${G}$ -invariant probability measure from ${G/\Gamma}$ to ${G/Z}$ . It must be supported on a fixed point, i.e. ${G/Z}$ is a point.

1.4. Generalization

Fix a locally compact sigma-compact group ${\Gamma}$ and a representation ${\rho:\Gamma\rightarrow G}$ . Then ${\Gamma}$ acts on ${V}$ . The orbit space is complicated, but still ${V\rightarrow V/G}$ is a ${\Gamma}$ -map. Same reasoning yields: every ${\Gamma}$ -invariant ergodic measure is supported on a unique ${G}$ -orbit.

Theorem 6 There exists a minimal normal ${k}$ -subgroup ${N<G}$ such that

$\displaystyle \Gamma\rightarrow G\rightarrow G/N$

has precompact image.
Every ${\Gamma}$ -invariant measure on a ${G}$ -algebraic variety is supported on the ${N}$ -fixed points.

Consider ${\Gamma=Stab_G(\mu)}$ , for ${\mu\in Prob(V)}$ .

Corollary 7 The stabilizer of a measure ${\mu\in Prob(V)}$ is compact modulo the fixator of the Zariski-support of ${\mu}$ .

Fact (Zimmer). The action of ${G}$ on ${Prob(V)}$ has locally closed leaves.

1.5. Some more ergodic theory

A Lebesgue space is a standard Borel space equipped with a measure class.

By a map from a Lebesgue space ${X}$ to a Borel space ${U}$ , we mean an equivalence class of Borel maps : ${X\rightarrow U}$ defined almost everywhere, up to almost everywhere equality. The space of such maps is denoted by ${L(X,U)}$ .

A morphism of Lebesgue spaces is a map which sends null sets to null sets.

Let ${S}$ be a locally compact second countable group. Then ${S}$ has a standard Borel space structure and a Lebesgue space structure. An ${S}$ -Lebesgue space ${X}$ is a Lebesgue space with a homomorphism ${S\rightarrow Aut(X)}$ such that ${S\times X\rightarrow X}$ is a morphism.

An action of ${S}$ on ${X}$ is ergodic if every ${S}$ -invariant map ${X\rightarrow U}$ is essentially constant, for every standard Borel space ${U}$ .

Definition 8 Fix an action of ${S}$ on ${X}$ . Say it is

Doubly ergodic if the diagonal action on ${X\times X}$ is ergodic.

metrically ergodic if for every isometric action of ${S}$ on a separable metric space ${U}$ , every ${S}$ -equivariant map ${X\rightarrow U}$ is (essentially) constant.

Weakly mixing if for every ergodic probability measure preserving action of ${S}$ on ${Y}$ , the diagonal action on ${X\times Y}$ is ergodic.

Has no compact factors if for every continuous homomorphism ${S\rightarrow K}$ to a compact group ${K}$ and any compact subgroup ${H<K}$ , for every map ${X\rightarrow K/H}$ (equipped with Haar measure), ${H=K}$ .

Easy fact. ${1\implies 2\implies 3\implies 4}$ .

Indeed, if ${X}$ is doubly ergodic and acts isometrically on ${U}$ , the distance defines an invariant function on ${X\times X}$ , hence constant. If the constant is not zero, the ilage of ${X}$ is discrete in ${U}$ , hence countable (since ${U}$ is separable), contradiction.

If ${X}$ is metrically ergodic and has a pmp action on ${Y}$ , an invariant function ${f}$ on ${X\times Y}$ gives rise to an equivariant map ${X\rightarrow L^\infty(Y)}$ . Since probability measure is invariant, ${L^\infty(Y)\rightarrow L^2(Y)}$ is equivariant and the action on ${L^2(Y)}$ is isometric. Now ${L^2(Y)}$ is separable, so ${f}$ is constant.

If ${X}$ is weakly mixing and ${K/H}$ is a compact factor, one can assume ${X=K/H}$ . Take ${Y=K}$ . The map ${(x,k)\mapsto k^{-1}x}$ is ${K}$ -equivariant ${:X\times Y=(K/H)\times K\rightarrow K/H}$ , hence constant, so ${K/H}$ is a single point.

Easy fact. If the action of ${S}$ on ${X}$ is probability measure preserving, then ${1\iff 2\iff 3\iff 4}$ .

Indeed, it suffices to prove that ${4\implies 2}$ . One can assume that metric space ${U}$ has an invariant probability measure ${\mu}$ , fully supported, and that ${U}$ is complete. One easily shows that ${U}$ is compact. Then ${K=Isom(U)}$ is compact. It must act transitively on ${U}$ , ${U=K/H}$ . Under assumption 4, ${U}$ is a point, this is ${2}$ .

1.6. metric ergodicity

Nonexample. Let ${K<G}$ be a compact subgroup. Let ${S\rightarrow G}$ be a homomorphism. Then the action of ${S}$ on ${G/K}$ is not metrically ergodic.

Example. Let ${\Gamma}$ be a countable group. Let ${\Omega}$ be a probability space. Then the shift action of ${\Gamma}$ on ${\Omega^\Gamma}$ is metrically ergodic.

Indeed, ${\Omega^\Gamma \times \Omega^\Gamma =(\Omega\times\Omega)^\Gamma}$ , and the shift action on ${(\Omega\times\Omega)^\Gamma}$ is ergodic.

Claim. Let ${G}$ be a noncompact ${k}$ -simple algebraic group. Let ${\Gamma <G}$ be a lattice, ${H<G}$ a noncompact closed subgroup. Then the action of ${\Gamma}$ on ${G/H}$ and the action of ${H}$ on ${G/\Gamma}$ is metrically ergodic.

Indeed, metric ergodicity passes to lattices (pass from ${U}$ to ${Map_\Gamma(S,U)}$ ). For the ${H}$ action, this follows from Howe-Moore. Indeed, the action of ${G}$ on the pmp space ${G/\Gamma}$ is mixing. This implies decay of coefficients. Their restrictions to any closed noncompact subgroup ${H}$ decay, hence the mixing action of ${H}$ .

1.7. Amenability

Definition 9 (Zimmer) The action of ${S}$ on ${X}$ is amenable if there exists an ${S}$ -equivariant conditional expectation

$\displaystyle L^\infty(S\times X) \rightarrow L^\infty(X).$

Note that amenability implies the following weaker “baby amenability”, which is often used: for every compact convex ${S}$ -space ${C}$ , there exists an ${S}$ -map ${X\rightarrow C}$ .

Example. If ${H<S}$ is an amenable subgroup, the action of ${S}$ on ${S/H}$ is amenable.

Fact. For every locally compact second countable group ${S}$ , there exists an action of ${S}$ on some Lebesgue space ${X}$ which is both amenable and metrically ergodic (the Furstenberg boundary).

Example. Let ${G}$ be a noncompact ${k}$ -simple algebraic group. Let ${\Gamma <G}$ be a lattice, let ${H<G}$ be a noncompact amenable subgroup. Then the action of ${\Gamma}$ on ${G/H}$ is both amenable and metrically ergodic.

2. Algebraic representations of ergodic actions

Now we merge algebraic groups and ergodic actions. Fix a locally compact second countable group ${S}$ , an action of ${S}$ on a Lebesgue space ${X}$ , a local field ${k}$ and an algebraic ${k}$ -group ${\mathbb{G}}$ , ${G=\mathbb{G}(k)}$ . Fix a continuous homomorphism ${\rho:S\rightarrow G}$ .

Definition 10 An algebraic representation of the action of ${S}$ on ${X}$ with respect to ${\rho}$ is a ${k}$ – ${\mathbb{G}}$ -variety ${\mathbb{V}}$ and an ${S}$ -equivariant map ${\phi:S\rightarrow V=\mathbb{V}(k)}$ .
A morphism between to such AREAs ${(\mathbb{V},\phi)}$ and ${(\mathbb{U},\psi)}$ is a ${k}$ – ${\mathbb{G}}$ -morphism ${\alpha:\mathbb{V}\rightarrow\mathbb{U}}$ such that ${\alpha\circ\phi=\psi}$ .

Example. Let ${T<S}$ be a closed subgroup. Consider the action of ${S}$ on ${T/S}$ . Every algebraic representation of this action is given by a pair ${\mathbb{G},\mathbb{V})}$ and a point in ${V}$ which is fixed by the Zariski closure of ${\rho(T)}$ in ${G}$ .

If ${\rho}$ is Zariski dense, we get a map from ${V_0=G/H_0}$ to ${V}$ , where

$\displaystyle H_0=\overline{\rho(T)}^Z.$

We get an AREA ${\phi_0:X=S/T\rightarrow V_0}$ , and for every AREA ${\phi:X\rightarrow V}$ , we have a unique morphism ${V_0\rightarrow V}$ such that ${\phi=\alpha\circ\phi_0}$ .
In other words, ${G/H_0}$ is an initial object in the category of AREAs of ${S/T}$ . This holds in general.

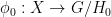
Theorem 11 Let ${S}$ act ergodically on ${X}$ . Then there exists an initial object in the category of AREAs associated with ${\rho}$ , of the form ${\phi_0:X\rightarrow G/H_0}$

We think of an ergodic action of ${S}$ as a generalization of a closed subgroup, up to conjugacy. The theorem states that the initial object is indeed a Zariski-closed subgroup.

Proof of Theorem 11. Consider the set of ${k}$ -algebraic subgroups of ${G}$ such that there exists a, AREA ${\phi:X\rightarrow G/H}$ . This is nonempty. By Noetherianity, one can pick a minimal element ${H_0}$ (it will turn out to be a minimum, up to conjugacy, but it is harder). We show that the map ${\phi_0:X\rightarrow G/H_0}$ is an initial object.

Consider an other AREA ${\phi:X\rightarrow V}$ . Consider the diagonal representation

$\displaystyle \phi\times\phi_0:X\rightarrow V\times G/H_0 .$

By ergodicity, the image of ${X}$ lies in one single ${G}$ -orbit ${G/H_1}$ . Composing with projection, we get a ${G}$ -map ${G/H_1 \rightarrow G/H_0}$ , hence an embedding ${H_1 < H_0}$ up to conjugacy. By minimality, ${H_1=H_0}$ . The other projection ${G/H_1\rightarrow V}$ provides us with a ${G}$ -map ${G/H_0\rightarrow V}$ , which is unique.

Theorem 12 Assume the action of ${S}$ on ${X}$ is pmp, ${\mathbb{G}}$ is ${k}$ -simple and ${\rho(S)}$ is unbounded (i.e. not contained in a compact subgroup). Then the initial object is trivial: any representation of ${X}$ is constant. Indeed, an ${S}$ -invariant probability measure on ${V}$ exists only if ${\rho(S)}$ is precompact.

2.1. Consequences

Theorem 13 (Bader-Furman-Gorodnik-Weiss) Let ${G}$ be a noncompact ${k}$ -simple algebraic group. Let ${\Gamma <G}$ be a lattice, let ${H<G}$ be a noncompact ${k}$ -algebraic subgroup. Consider the ${\Gamma}$ -action on ${G/H=X}$ . For ${\rho=}$ the inclusion of ${\Gamma}$ into ${G}$ , the initial object is the identity ${X=G/H}$ .

Application. Every Borel map ${{\mathbb R}^n\rightarrow{\mathbb R}^n}$ which commutes with ${SL_n({\mathbb Z})}$ is a homothety.

Indeed, let ${\phi:G/H\rightarrow G/H=V}$ be a ${\Gamma}$ -map. Let ${\Phi}$ be the composition of ${\phi}$ with ${G\rightarrow G/H}$ . Set

$\displaystyle \Psi:G\rightarrow V,\quad \Psi(g)=g^{-1}\Phi(g).$

Then ${\Psi}$ is right- ${\Gamma}$ -invariant and left- ${H}$ -invariant. Since the action of ${H}$ on ${G/\Gamma}$ is pmp and weakly mixing, ${\Psi}$ is constant. Thus there exists ${v\in V}$ such that ${g^{-1}\Phi(g)=v}$ , ${\Phi(g)=gv}$ , i.e. ${\phi}$ is a ${G}$ -map.

Theorem 14 Let ${X}$ be an amenable and metrically ergodic ${S}$ -space. Let ${\mathbb{G}}$ be a ${k}$ -simple algebraic group. Let ${\rho:S\rightarrow G}$ be an unbounded homomorphism. Then there exists an initial object ${\phi:X\rightarrow G/H}$ where ${H<G}$ is a proper subgroup.

Indeed, let ${P}$ be a parabolic subgroup of ${G}$ . Since ${S}$ acts on the convex space ${Prob(G/P)}$ , by amenability, there exists an ${S}$ -map ${X\rightarrow Prob(G/P)}$ . Since ${G}$ -orbits in ${Prob(G/P)}$ are locally closed, the image of the ${S}$ -map is contained in a single orbit ${G/H_1}$ , where ${H_1}$ is the stabilizer of a measure ${\mu}$ . By the structure theorem on measure stabilizers, the fixator ${H_0}$ of the Zariski hull of the support of ${\mu}$ is cocompact in ${H_1}$ . Up to conjugacy, it is contained in ${P}$ .

Assume that ${H_0}$ is trivial. Then ${H_1}$ is compact, ${G}$ acts by isometries on the separable space ${G/H_1}$ . By metric ergodicity, the ${S}$ -map ${X\rightarrow G/H_1}$ is constant, which contradicts the assumption that ${\rho(S)}$ is unbounded in ${G}$ .

Therefore, ${H_0}$ is not normal. ${H_1}$ is contained in the normalizer ${N}$ of ${H_0}$ in ${G}$ , which is a proper ${k}$ -algebraic subgroup of ${G}$ . The composition ${X\rightarrow G/H_1 \rightarrow G/N}$ is a nontrivial AREA for ${X}$ with respect to ${\rho}$ .

3. Lattices in products

Today, we are aiming at rigidity results for lattices. Before entering the subject, let me sum up where we had reached last time.

3.1. AREAs continued

The tension between ergodicity and the very simple structure of algebraic actions creates an initial object in the category of AREAs. We call gate the initial object, because it is our entrance gate into the algebraic world.

Two theorems:

Theorem 12. For a pmp and metrically ergodic action, the gate is trivial.
Theorem 14. For amenable and metrically ergodic actions, the gate is nontrivial.

Remark: unbounded amenable subgroups of ${G}$ are not Zariski-dense.

3.2. Leftover from last time : functoriality

Proposition 15 Fix ${\rho:S\rightarrow G}$ . The gate defines a functor from the category of ${S}$ -ergodic actions and the category of ${k}$ -algebraic ${G}$ -(coset)-varieties.

3.3. Introduction to lattices in products

Examples.

${{\mathbb Z}[\sqrt{2}]}$ is a lattice in ${{\mathbb R}\times{\mathbb R}}$ .

${{\mathbb Z}[\frac{1}{p}]}$ is a lattice in ${{\mathbb R}\times{\mathbb Q}_p}$ .

${SL_n({\mathbb Z}[\frac{1}{p}])}$ is a lattice in ${SL_n({\mathbb R})\times SL_n({\mathbb Q}_p)}$ .

Definition 16 A lattice ${\Gamma}$ in a product ${S=S_1\times S_2}$ is irreducible if its projections to both factors are dense subgroups.
Equivalently, the action of ${\Gamma}$ on each factor is ergodic.

Equivalently, the actions of ${\Gamma\times S_2}$ and of ${S_1\times \Gamma}$ on ${S_1\times S_2}$ are ergodic.

Equivalently, the action of each ${S_i}$ on ${(S_1\times S_2)/\Gamma}$ is ergodic.

Indeed, the action of ${S_i}$ on ${L^\infty(S_i)}$ equipped with the weak ${^*}$ topology is continuous.

3.4. Commensurability

Assume that ${S}$ is totally disconnected locally compact. Then there exists a compact open subgroup ${K<S}$ . Any two are commensurable. Say a subgroup ${K<S}$ is commensurated if for all ${s\in S}$ , ${K^s}$ and ${K}$ are commen surable.

Let ${\Gamma<S_1\times S_2}$ be an irreducible lattice. Let ${K_1<S_1}$ be a compact open subgroup. Then

$\displaystyle \Lambda=\gamma\cap(K_1\times S_2).$

is commensurated in ${\Gamma}$ , it is a lattice in ${K_1\times S_2}$ . Hence ${\Lambda<S_2}$ is a lattice which is commensurated by the dense subgroup ${\Gamma<S_2}$ .
Conversely, assume that ${\Lambda<\Gamma<T}$ where ${\Lambda<T}$ is a lattice, ${\Lambda<\Gamma}$ is commensurated and ${\Gamma<T}$ is dense. Then one can reconstruct ${S_1}$ from these data. There exists a totally disconnected group ${T'}$ , a dense embedding ${\Gamma\rightarrow T'}$ , and a precompact embedding ${\Lambda\rightarrow T'}$ such that ${\Gamma<T\times T'}$ is an irreducible lattice. It is called the Schlichting completion of ${(\Gamma,\Lambda)}$ .

This indicates that lattices in products Lie ${\times}$ tdlc are simpler that lattices in Lie groups, in the sens that we have a dual way of looking at them.

3.5. Superrigidity

Theorem 17 Let ${\Gamma<S_1\times S_2}$ be an irreducible lattice. Let ${G}$ be a ${k}$ -simple group, let ${\rho:\Gamma\rightarrow G}$ is Zariski dense and unbounded. Then superrigidity holds: ${\rho}$ extends uniquely to a continuous homomorphism ${\bar\rho:S\rightarrow G}$ and ${\bar \rho}$ factors through one of the factors.

Corollary 18 If ${\Lambda<\Gamma<T}$ are as above (i.e. ${\Lambda<\Gamma}$ is commensurated and ${\Gamma<T}$ is dense), ${G}$ is ${k}$ -simple and ${\rho:\Gamma\rightarrow G}$ is Zariski dense and unbounded on ${\Lambda}$ , then ${\rho}$ extends uniquely to a continuous homomorphism ${\bar\rho:T\rightarrow G}$ .

Indeed, the case where ${\rho}$ extends to ${T'}$ is excluded.

3.6. Application to arithmeticity

Apply previous theorem to a lattice in ${G}$ and conclude that a lattice ${\Gamma<G}$ is arithmetic iff it has a dense commensurator.

3.7. Preparation for the proof

Fix an action of ${S_i}$ on a Lebesgue space ${B_i}$ which is amenable and metrically ergodic.

Claim. The diagonal action of ${S_1\times S_2}$ on ${B_1\times B_2}$ is amenable and metrically ergodic.

Indeed, assume ${C}$ is a nonempty ${S}$ -compact convex space. Then ${Map_{S_1}(B_1,C)}$ is nonempty, it is an ${S_1}$ -compact convex space (viewed as a subset of ${L^\infty(B_1,C)}$ ). Therefore, there exists an ${S_2}$ -map ${B_2\rightarrow Map_{S_1}(B_1,C)}$ . I.e., there exists an ${S_1\times S_2}$ -map ${B_1\times B_2\rightarrow C}$ . This proves amenability.

Let ${U}$ be an ${S}$ -isometric metric space. Any ${S}$ -map ${B_1\times B_2\rightarrow U}$ is a.e. independant on the ${B_1}$ variable, and on the ${B_2}$ variable, therefore a.e. constant.

Corollary 19 For every irreducible lattice in ${S}$ , the action of ${\Gamma}$ on ${B_1\times B_2}$ is amenable and metrically ergodic.

Of course, the action of ${\Gamma}$ on ${S}$ is not ergodic, it is proper, but

Claim. The action of ${\Gamma}$ on ${S_1\times B_2}$ is ergodic.

Before proving the claim, let us start with a general fact.

Given an action of ${S}$ on ${X}$ , when is the restriction to ${\Gamma}$ ergodic? Answer is : iff the action of ${S}$ on ${(S/\Gamma)\times X}$ is ergodic. Indeed, one can mod out by a proper action: the space of ${\Gamma}$ -orbits in ${S\times X}$ , denoted by ${S\times_\Gamma X}$ , is well defined, since the diagonal ${S}$ -action on ${S\times X}$ is conjugated to the action on the ${S}$ -factor only, trivial on the ${X}$ factor. In fact, ${S\times_\Gamma X=(S/\Gamma)\times X}$ .

Applying this to the claim, ${\Gamma}$ ergodic on ${S_1\times B_2}$ ${\iff}$ ${S}$ ergodic on ${(S/\Gamma)\times S_1\times B_2}$ ${\iff}$ ${S_2}$ ergodic on ${(S/\Gamma)\times B_2)}$ is implies by metric ergodicity of ${S_2}$ on ${B_2}$ .

This proves the claim.

3.8. Proof of superrigidity theorem

Again, fix an action of ${S_i}$ on a Lebesgue space ${B_i}$ which is amenable and metrically ergodic. The action of ${\Gamma}$ on ${B_1\times B_2}$ is amenable and metrically ergodic. According to Theorem 14, the gate ${G/H}$ is nontrivial, i.e. ${H\not=G}$ .

Pick a generic ${S_1}$ -orbit in ${B_1\times B_2}$ , identify it with ${S_1}$ . Get a map ${S_1\times B_2\rightarrow G/H}$ . The ergodic action of ${\Gamma}$ on ${S_1\times B_2}$ yields a gate ${\theta:\Gamma\times S_1 G\times N/H_0}$ , ${N}$ the normalizer of ${H_0}$ in ${G}$ . Mod out by ${N}$ , get a ${\Gamma\times S_1}$ -map ${S_1\times B_2\rightarrow G/N}$ . By ergodicity, we get a map ${B_2\rightarrow G/N}$ .

3.9. Assume that ${H_0\not=\{e\}}$

By simplicity of ${G}$ , ${N\not=G}$ . So the ${\Gamma}$ -action on ${B_2}$ has a nontrivial representation ${B_2\rightarrow G/N}$ , whence a ${\Gamma}$ -representation ${S_2\rightarrow G/N}$ . There exists a gate ${S_2\rightarrow G/H_2}$ where ${N_2<N\not=G}$ . By ergodicity of the ${\Gamma}$ -action on ${S_2}$ , we get a ${\Gamma\times S_2}$ -equivariant map (where ${\Gamma\times S_2\rightarrow G\times N_2/H_2}$ , where ${N_2}$ is the normalizer of ${H_2}$ ) from ${S_2}$ to ${G/N_2}$ . Again by ergodicity, there is a ${\Gamma}$ -invariant point in ${G/N_2}$ . It also fixed by the Zariski-closure of ${\Gamma}$ , which is ${G}$ . Hence ${N_2=G}$ , ${H_2}$ is normal in ${G}$ . By simplicity, ${H_2=\{e\}}$ . So the above morphism to ${G\times N_2/H_2}$ was to ${G\times G}$ . The formula

$\displaystyle s_2 \mapsto \phi(s_2)\theta_2(s_2)^{-1}$

defines an ${S_2}$ -invariant (hence constant) map ${S_2\rightarrow G}$ . In other words, ${\phi(s_2)=g\theta(s_2)}$ . This implies that ${\rho=\theta_2^g}$ . Composing with the projection ${S\rightarrow S_2}$ , we get ${\bar\rho:S\rightarrow G}$ whose restriction to ${\Gamma}$ equals ${\rho}$ . So we are done under the assumption that ${H_0\not=\{e\}}$ . This was the easiest case.

3.10. From no on, assume that ${H_0=\{e\}}$

Then ${N=G}$ , so ${\theta:S_1\rightarrow G}$ . We have an ${\Gamma\times S_1}$ -equivariant map ${S_1\times B_2\rightarrow G}$ (equivariant w.r.t. ${\rho\times\theta:\Gamma\times S_1\rightarrow G\times G}$ ).

Compose this map with ${G\times G\rightarrow G\times G/\Delta}$ , the diagonal. This is an AREA of ${\Gamma\times S_1}$ to ${G\times G}$ . By ergodicity of ${\Gamma\times S_1}$ on ${S_1\times S_2}$ , there is a gate ${S_1\times S_2\rightarrow G\times G/M}$ where ${M<\Delta}$ . Let us show that we are done if ${M\not=\Delta}$ .

Assume that ${M\not=\Delta}$ . Let us mod out the left ${G}$ -action. This mods out the ${S_1}$ -action in the gate, thus I get an ${S_2}$ -map from ${S_2}$ to a nontrivial quotient of ${G}$ . As before, we get an extension of ${\rho}$ to ${S}$ .

From now on, assume that ${M=\Delta}$ . ${S_2}$ acts on ${S_1\times S_2}$ . Since ${\Delta}$ is equal ti its own normalizer in ${G\times G}$ , the gate factors via a map ${S_1\rightarrow S\times G/\Delta=G}$ , so ${\rho}$ extends as before.

4. Margulis superrigidity

Let ${S}$ be a real semisimple group of higher rank, let ${\Gamma<G}$ be an irreducible lattice. Margulis superrigidity states that every Zariski-dense unbounded homomorphism ${\rho:\Gamma\rightarrow G}$ uniquely extends to ${S}$ .

The case when ${S}$ is a product has been treated. Next time, I will prove the case when ${S}$ is simple. I explain now that we are not too far from it.

Consider ${S=SL_3(\ell)}$ , ${T=\{\begin{pmatrix} \lambda & 0 & 0 \\ 0 & \lambda & 0 \\ 0 & 0 & \lambda^{-2} \end{pmatrix} \,;\, \lambda\in\ell\}}$ . It is amenable, noncompact, and its centralizer is the upper diagonal ${GL_2(\ell)}$ . The ${\Gamma}$ -action on ${S/T}$ is amenable and metrically ergodic. ${\Gamma\times PGL_2(\ell)}$ acts on ${S/T}$ and we get a gate ${S/T\rightarrow G/H}$ .

I would like to indicate a related geometric context without groups acting, that of ${\tilde A_2}$ -buildings, covered by Caprace-Lecureux. At infinity, such buildings have an exotic projective plane. It has a large group of projectivities (in fact a pseudogroup of maps from lines to lines). This yields a large group acting on the boundary of a tree. It plays the role of ${PGL_2(\ell)}$ . It is not too hard to show that this group is linear iff the building is classical. It follows that ${\Gamma}$ is linear iff the building is classical.

4.1. Remarks on lattices in products

The superrigidity theorem holds for lattices in products of ${n}$ factors for any ${n}$ .
Nonarithmetic examples are known only for ${n=2}$ yet.
The examples are Kac-Moody groups acting on twin buildings and Burger-Mozes and Wise examples acting on products of trees.

4.2. A new category of representations

For the proof of Margulis superrigidity, we need to modify the concept of AREA. Up to now, we represented an ${S}$ action on Lebesgue space ${X}$ . Now we need to represent pairs of closed subgroups of a locally compact second countable group ${S}$ .

The objects in our category are now the following data:

two closed subgroups ${\Gamma}$ and ${T}$ of ${S}$ ,
an algebraic ${k}$ -group ${G}$ ,
a ${k}$ -algebraic subgroup ${L<Aut_k(V)}$ that commutes with ${G}$ ,
a homomorphism ${\rho:\Gamma\rightarrow G}$ and a continuous and Zariski-dense homomorphism ${\theta:T\rightarrow L}$ ,
a representation, i.e. a measurable map ${\phi:S\rightarrow V}$ which is ${\rho\times\theta}$ -equivariant.

Theorem 20 Let ${\Gamma<S}$ be a lattice. Assume that the action of ${T}$ on ${S/\Gamma}$ is ME. Then there exists an initial object (a gate), i.e. a ${\Gamma\times T}$ -equivariant map

$\displaystyle S\rightarrow G/H_0,$

where ${\rho\times\theta:\Gamma\times T\rightarrow (G\times N)/H_0}$ and ${N=Norm_G(H_0)}$ .

The proof follows similar lines as Theorem 11. Pick a minimal ${H_0}$ .

4.3. The nontriviality theorem

Theorem 21 Let ${\Gamma<S}$ be a lattice. Assume that the action of ${T}$ on ${S/\Gamma}$ is ME. Assume further that ${T<S}$ is amenable, ${G}$ is ${k}$ -simple and ${\rho}$ is unbounded, then the gate is not trivial.

Indeed, consider the ${\Gamma}$ action on ${X=S/T}$ . By amenability and ME, there exists a proper subgroup ${H<G}$ and a representation ${S\rightarrow S/T\rightarrow G/H}$ , under homomorphism ${\rho\times e:\Gamma\times T\rightarrow G\times\{e\}}$ . The gate will be a deeper object, but this suffices to prove that the gate is nontrivial.

4.4. Functoriality

Assume that ${S}$ is a noncompact simple ${\ell}$ -algebraic group. Let ${\Gamma<S}$ be a lattice. Recall that for every closed noncompact ${T<S}$ , the actions of ${\Gamma}$ on ${S/T}$ and of ${T}$ on ${S/\Gamma}$ are ME (this is Howe-Moore’s theorem). We now show that this gives right to extra invariants.

Fix ${S}$ , ${\Gamma}$ . Consider the category of ${(\Gamma,S)}$ -actions, i.e.

the objects are closed, noncompact subgroups ${T<S}$ ,
the morphisms are elements ${s}$ of ${S}$ acting on the right and conjugating the right action of ${T_1}$ into the right action of ${T_2}$ on ${S}$ .

Consider next the category of ${G}$ -spaces:

the objects are ${L}$ ‘s acting on ${G}$ -space ${V}$ , commuting with ${G}$ ,
the morphisms are ${k}$ – ${G}$ -morphisms of varieties ${V\rightarrow U}$ .

The gate functor assigns to a ${(\Gamma,S)}$ -action of ${\Gamma\times T_1}$ on ${S}$ an orbit ${G/H_1}$ with action of ${G\times N/H_1}$ . To a morphism ${S\rightarrow S}$ given by element ${s\in S}$ , the gate associates a unique morphism ${\alpha(s)=gate(s)}$ of algebraic varieties ${G/H_1\rightarrow G/H_2}$ .
In particular, we get a map ${\alpha:Aut(\Gamma,S,T)\rightarrow Aut(G/H_0)}$ . The group ${Aut(G/H_0)=N_G(H_0)/H_0}$ . On the other hand, ${Aut(\Gamma,S,T)=N_S(T)}$ . This homomorphism ${\alpha}$ is a nontrivial datum: it gives extra invariance to the representation ${S\rightarrow G/H_0}$ .

Corollary 22 If ${T_1,T_2<S}$ normalize each other. Then they have the same gate ${S\rightarrow G/H_0}$ .

I really mean, the same map serves as a gate for both.

4.5. Proof of Margulis superrigidity

Recall our goal. Let ${S}$ be a real semisimple group of higher rank, let ${\Gamma<G}$ be an irreducible lattice. Margulis superrigidity states that every Zariski-dense unbounded homomorphism ${\rho:\Gamma\rightarrow G}$ uniquely extends to ${S}$ .

Fact. There exist closed noncompact abelian subgroups ${T_1,\ldots,T_n<S}$ generating ${S}$ such that each ${T_i}$ commutes with ${T_{i+1}}$ .

In fact, this is equivalent to higher rank.

Example. ${S=SL_3({\mathbb R})}$ . The first three ${T_i}$ ‘s are ${1}$ -parameter subgroups of the Heisenberg group of upper unipotent matrices, the three next are ${1}$ -parameter subgroups of the opposite Heisenberg group of lower unipotent matrices.

Geometrically speaking, it means that one can move from any geodesic to any other by travelling within finitely many maximal flats.

Now we embark in the proof. By Corollary 22, all the ${T_i}$ ‘s have the same gate ${\phi:S\rightarrow G/H}$ , equivariant with respect to ${\rho\times\theta_i:\Gamma\times T_i \rightarrow G\times N/H}$ . By ergodicity, the ${\Gamma}$ -invariant point is invariant under the Zariski closure of ${\rho(\Gamma)}$ , i.e; b y ${G}$ , so ${N=G}$ , ${H}$ is normal in ${G}$ . Since ${T_i}$ is amenable, ${H\not=G}$ so ${H=\{e\}}$ .

So the gate is ${\phi:S\rightarrow G}$ , equivariant with respect to ${\rho\times\theta_i:\Gamma\times T_i \rightarrow G\times G}$ .

${\phi}$ defines a pull-back map from the algebra of polynomial functions on ${G}$ , ${k[G]}$ , to ${k}$ -valued functions on ${S}$ , ${L(S,k)}$ . It is injective, since its Zariski support is ${G}$ . This embeds ${k[G]}$ as a ${T_i}$ -invariant subalgebra of ${L(S,k)}$ for all ${i}$ , hence an ${S}$ -invariant subalgebra. This gives an ${S}$ -action of ${S}$ on ${k[G]}$ extending the actions of the ${T_i}$ . Thus ${S}$ acts on ${G}$ on the right, when a homomorphism ${\theta:S\rightarrow G}$ . The gate ${\phi:S\rightarrow G}$ is ${\rho\times\theta}$ -equivariant, this implies that ${\rho}$ extends to ${S}$ . End of proof.

4.6. Rank one

Let ${S}$ be a real semisimple group of rank one, let ${\Gamma<G}$ be an irreducible lattice. Let ${\rho:\Gamma\rightarrow G}$ be a Zariski-dense unbounded homomorphism. What extra assumptions should we make to show that ${\rho}$ extends?

For ${T<S}$ , let ${\phi_T}$ , ${\theta_T}$ , ${N_T}$ , ${H_T}$ ,… denote the ${T}$ -gate.

Lemma 23 Let ${T=P=MAU}$ be a parabolic. If ${H_P=\{e\}}$ , then ${\rho}$ extends.

Indeed, consider ${\phi_A}$ , ${H_A<H_P}$ hence ${H_A=\{e\}}$ , ${\phi_A=\phi_{N_S(A)}}$ .

Since ${P}$ and ${N_S(A)}$ generate ${S}$ , ${\rho}$ extends as before.

Lemma 24 Assume that there exists a simple, noncompact subgroup ${W<S}$ and a ${\Gamma}$ -representation ${S/W\rightarrow G/H}$ , equivariant with respect to ${\rho}$ , with ${H\not=G}$ . Then ${U}$ is not in the kernel of ${\theta_P}$ .

Indeed, ${U'=W\cap U}$ is noncompact. By a finite number of up and down steps of taking normalizers we reach ${P}$ (two steps should be sufficient). All these intermediate normalizers have the same gate. Assume by contradiction that ${\theta_P(U)=\{e\}}$ . Then the ${U'}$ -gate equals the ${P}$ -gate, which thus factors by ${U}$ . This map is both ${U}$ and ${W}$ -invariant, but ${U}$ and ${W}$ generate ${S}$ . Thus ${H=G}$ , contradiction.

Note that the assumption of Lemma 24 never holds if ${U<\mathrm{ker}(\theta_P)}$ and ${K}$ is nonarchimedean.

4.7. Relation to arithmeticity

Definition 25 Say that ${G}$ is compatible (with ${S}$ ) if for all proposer subgroups ${H}$ of ${G}$ , ${U<\mathrm{ker}(\theta_P)}$ , where ${\theta_P:P\rightarrow N_G(H)/H}$ .

Let ${S=\mathbb{S}({\mathbb R})}$ where ${S\not=Sl(2,{\mathbb R})}$ . Le ${\Gamma<S}$ ne an orreducible lattice.

Fact. There exists a unique minimal number field ${i_0:\ell\rightarrow{\mathbb R}}$ such that ${S}$ is defined over ${\ell}$ and ${\Gamma<S(\ell)}$ up to conjugation and finite index.

Theorem 26 (Margulis arthmeticity criterion) ${\Gamma}$ is arithmetic if and only iff its image is precompact in any place other than ${i_0}$ . I.e. for every embedding ${j:\ell\rightarrow k}$ to a local field, either ${j(\Gamma)\subset\mathbb{S}(k)}$ is precompact or ${k={\mathbb R}}$ and ${j=i_0}$ .

Supperrigidity implies arithmeticity. Indeed, take ${\mathbb{G}=\mathbb{S}}$ . Can assume that it is adjoint. For every embedding ${j:\ell\rightarrow k}$ , the image of the composition ${\Gamma \rightarrow\mathbb{S}(\ell)\rightarrow\mathbb{S}(k)}$ is precompact unless ${S=\mathbb{S}({\mathbb R})}$ . By an argument of Borel-Tits, one gets ${j=i_0}$ .

Observe that one need only a few targets ${\mathbb{G}}$ to get arithmeticity.

Theorem 27 (Bader-Fisher-Miller-Stover) If there exists in ${\Gamma\setminus S/K}$ infinitely many immersed maximal totally geodesic subspaces of dimension ${\geq 2}$ , then the assumption of Lemma 24 holds for all ${\mathbb{G}}$ ‘s relevant to arithmeticity.

Corollary 28 ${\Gamma}$ is defined over the ring of integers of a number field.

Exercise. For ${n\geq 4}$ , ${S=SO(n,1)}$ , the group ${\mathbb{G}=\mathbb{S}({\mathbb C})}$ is compatible. In particular, if there exist infinitely many immersed maximal totally geodesic subspaces of dimension ${\geq 2}$ , then ${\Gamma}$ is arithmetic. (Special care is needed for ${n=3}$ ).

5. Apafic Gregs

Talk given in Fanny Kassel’s seminar, on Oct. 11th, 2021, dedicated to Margulis, Perlman and Baldi.

Joint work with Alex Furman.

How to produce a random element of a group? In fact, a sequence. We will study linear representations of such random elements.

5.1. GREGs

Definition 29 Let ${X}$ be a probability space. Let ${T}$ be an ergodic invertible pmp transformation of ${X}$ . Let ${\Gamma}$ be a locally compact second countable group. Let ${\phi:X\rightarrow\Gamma}$ be a map. The Greg is the data ${(X,B,m,T,\Gamma,\phi)}$ .

Examples.

Compact. Let ${X=\Gamma=S^1}$ , ${\phi=id}$ , ${T}$ an irrational rotation.

Random walk. Fix ${\Gamma}$ and a probability measure ${\mu}$ on ${\Gamma}$ . Let ${X=\Gamma^{\mathbb Z}}$ , ${T=}$ shift, ${\phi=}$ projection to the ${0}$ -th coordinate. The resulting Greg is a random walk.

Markov chain. Fix a graph with probability transitions (i.e. for each vertex ${v}$ , a probability measure on the set of edges emanating from ${v}$ ), ${X=}$ set of paths in the graph, ${m=}$ some Gibbs measure associate. Decorate edges with elements of ${\Gamma}$ . This defines a map ${\phi:X\rightarrow \Gamma}$ .

Geodesic flow. Let ${M}$ be a compact negatively curved Riemannian manifold. Let ${X=T^1 M}$ denote the unit tangent bundle of ${M}$ . ${T_t=}$ geodesic flow. Let ${\Gamma=\pi_1(M)}$ . Fix a fundamental domain. For each time ${t}$ , there is a map ${\phi_t:X\rightarrow\Gamma}$ which tells which group element drags ${T_t(v)}$ back to the fundamental domain. One can decorate the picture with a flat bundle.

5.2. Associated constructions

Let ${B}$ be the minimal ${\sigma}$ -algebra such that ${\phi}$ is measurable. Given ${m<n}$ , let ${F_m^n=\bigvee_{k=m}^n T^k F}$ . Assume that ${B=F_{-\infty}^{+\infty}}$ .

Let ${X_+=F}$ equipped with the future ${\sigma}$ -algebra ${F_0^{+\infty}}$ . Let ${X_-=F}$ equipped with the past ${\sigma}$ -algebra ${F_{-\infty}^0}$ (I view these as factors of ${X}$ ). Then ${T}$ maps ${X_+\rightarrow X_+}$ , ${T^{-1}:X_-\rightarrow X_-}$ . It turns out that ${X}$ can be reconstructed from the pair ${(X_+,T)}$ , using the natural extension construction.

Definition 30 Let ${S:Y\rightarrow Y}$ be a pmp map which is not invertible. One constructs another system, with an invertible transformation, by taking the inverse limit ${\tilde Y}$ of

$\displaystyle \cdots\rightarrow Y\rightarrow Y\rightarrow Y\rightarrow\cdots$

Example. ${X=\Gamma^{\mathbb N}}$ , ${T=}$ shift, then the natural extension is ${\Gamma^{\mathbb Z}}$ .

Theorem 31 If ${T}$ is ergodic on ${Y}$ , then its natural extension ${\tilde T}$ on ${\tilde Y}$ is metrically ergodic.

Here, ${\tilde T}$ metrically ergodic means that for every metric extension ${U\rightarrow \tilde Y}$ (i.e. a family of complete separable metric spaces on which a lift of ${\tilde T}$ acts isometrically, there exists an equivariant section.

Fact. The map ${\phi:X\rightarrow \Gamma}$ defines a cocycle as follows. For ${n=0}$ , ${\phi_0=e}$ , and for ${n>0}$ ,

$\displaystyle \phi_n(x)=\phi(T^{n-1}x)\phi(T^{n-2}x)\cdots \phi(Tx)\phi(x),\quad \phi_{-n}(x)=\phi_n(T^{-n}x)^{-1}.$

The cocycle identity

$\displaystyle \phi_{n+m}(x)=\phi_n(T^m x)\phi_m(x)$

holds. Then a map ${X\times\Gamma\rightarrow\Gamma^{\mathbb Z}}$ is defined by

$\displaystyle (x,\gamma)\mapsto (\phi_n(x)\gamma^{-1}).$

Whence an action of ${{\mathbb Z}\times\Gamma}$ on ${\Gamma^{\mathbb Z}}$ .
The projections ${\Gamma^{\mathbb Z}\rightarrow\Gamma^{{\mathbb Z}_{\ge 0}}}$ and ${\Gamma^{\mathbb Z}\rightarrow\Gamma^{{\mathbb Z}_{\le 0}}}$ , when modded out by ${\Gamma}$ , yield the factors ${X\rightarrow X_+}$ and ${X\rightarrow X_-}$ . If instead one mods out by ${{\mathbb Z}}$ , one gets the space ${E}$ of ${{\mathbb Z}}$ -ergodic components of ${\Gamma^{\mathbb Z}}$ , and factors ${E\rightarrow E_+}$ and ${E\rightarrow E_-}$ . I think of these as ideal futures and pasts.

Theorem 32 ${E}$ , ${E_+}$ and ${E_-}$ are amenable ${\Gamma}$ -spaces, the maps ${E\rightarrow E_+}$ and ${E\rightarrow E_-}$ are ${\Gamma}$ -metrically ergodic.

5.3. Asymptotic past and future independence condition

Definition 33 Say that the asymptotic past and future independence condition (apafic) is satisfied if the map ${E\rightarrow E_+\times E_-}$ is measure class preserving.

In other words, if you were born poor, you still may become rich. It holds for all examples above but the compact example.

If the Greg is Apafic, then the pair ${(E_-,E_+)}$ is called a Boundary pair. The spaces are amenable and the maps ${E_+\times E_-\rightarrow E_+}$ and ${E_-}$ are metrically ergodic.

Theorem 34 Let ${G}$ be a simple ${k}$ -algebraic group. Let ${\rho:\Gamma\rightarrow G}$ be Zariski-dense. Then there exist opposite parabolic subgroups ${Q_+,Q_-<G}$ and measurable equivariant maps ${E_+\rightarrow G/Q_+}$ , ${E_-\rightarrow G/Q_-}$ and ${E_+\times E_-\rightarrow G/(Q_+\cap Q_-)}$ .
Moreover, if ${k={\mathbb R}}$ , ${Q_+=Q_-}$ is the minimal parabolic.

View the Cartan projection as a leftinvariant ${\mathfrak{a}^+}$ -valued metric on ${G}$ . Let ${F_n}$ be the composition of ${\phi_n:X\rightarrow \Gamma}$ with ${\rho}$ and Cartan projection,

$\displaystyle F_n:X\rightarrow \Gamma\rightarrow G\rightarrow \mathfrak{a}^+ .$

Subadditivity shows that ${\frac{1}{n}F_n}$ converges to an interior point of the Weyl chamber ${\mathfrak{a}^+}$ . This is called “simplicity of the spectrum”.
I view apafic gregs as a useful generalization of random walks, and we see that the simplicity of the spectrum theorem holds for them.

Tholozan, Ledrappier: See Avila-Viana for the Markov chain version.

> Let ${G}$ be a simple ${k}$ -algebraic group. Let ${\rho:\Gamma\rightarrow G}$ be Zariski-dense. Then there exist opposite parabolic subgroups ${Q_+,Q_-<G}$ and measurable equivariant maps ${E_+\rightarrow G/Q_+}$ , ${E_-\rightarrow G/Q_-}$ and ${E_+\times E_-\rightarrow G/(Q_+\cap Q_-)}$ .
Moreover, if ${k={\mathbb R}}$ , ${Q_+=Q_-}$ is the minimal parabolic.

View the Cartan projection as a leftinvariant ${\mathfrak{a}^+}$ -valued metric on ${G}$ . Let ${F_n}$ be the composition of ${\phi_n:X\rightarrow \Gamma}$ with ${\rho}$ and Cartan projection,

$\displaystyle F_n:X\rightarrow \Gamma\rightarrow G\rightarrow \mathfrak{a}^+ .$

Subadditivity shows that ${\frac{1}{n}F_n}$ converges to an interior point of the Weyl chamber ${\mathfrak{a}^+}$ . This is called “simplicity of the spectrum”.

I view apafic gregs as a useful generalization of random walks, and we see that the simplicity of the spectrum theorem holds for them.

Tholozan, Ledrappier: See Avila-Viana for the Markov chain version.

	metric2011 on Notes of Sa’ar Hersonsky…
	CH on Videos
	Stefan Wenger on Notes of Stefan Wenger’s…
	Stefan Wenger on Notes of Stefan Wenger’s…
	Stefan Wenger on Notes of Stefan Wenger’s…

Notes of Uri Bader IHES lectures october 5th, 2021

About metric2011

Leave a comment Cancel reply

Recent Posts

Recent Comments

Archives

Categories

Meta

Notes of Uri Bader IHES lectures october 5th, 2021

Share this:

Related

About metric2011

Leave a comment Cancel reply

Recent Posts

Recent Comments

Archives

Categories

Meta