Notes of Stefan Wenger’s lecture nr 2

Today, we shall prove the sharp gap theorem. Let me state it again.

Theorem 1 (Wenger 2008) Let ${X}$ be a geodesic metric space. Suppose

There exists a geodesic thickening ${Y}$ of ${X}$ with ${FA_0^{X,Y}\preceq r^2}$ ;

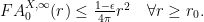
There exists ${\epsilon>0}$ and ${r_0 >0}$ such that $\displaystyle \begin{array}{rcl} FA_0^{X,\infty}(r)\leq \frac{1-\epsilon}{4\pi}r^2 \quad\forall r\geq r_0 . \end{array}$
Then ${X}$ is Gromov hyperbolic.

The assumption on existence of a thickening with quadratic filling is not restricitve. Indeed, we saw last time that Gromov guarantees extistence of such a thickening provided the coarse filling function is everywhere positive. This works for Cayley polyhedra, so we get

Corollary 2 Let ${\Gamma=\langle S|R \rangle}$ be a finitely presented group. If there exist ${\epsilon>0}$ and ${n_0 \in{\mathbb N}}$ such that for all ${n\geq n_0}$ ,

$\displaystyle \begin{array}{rcl} \delta_{\Gamma}(n)\leq\frac{1-\epsilon}{2\,\max\{|r|^2 \,;\, r\in R\}}n^2 , \end{array}$

then ${\Gamma}$ is Gromov hyperbolic.

1. Preparation

1.1. Asymptotic cones

Asymptotic cones reflect a metric space when we look at it from further and further away.

Let ${X}$ be a metric space. Pick a sequence of base points ${p_n \in X}$ and a sequence of scales ${r_n}$ . Define

$\displaystyle \begin{array}{rcl} \hat{X}=\{(x_n)\subset X\,;\,\sup_{n}\frac{1}{r_n}d(x_n , p_n) <\infty\} \end{array}$

We want to identify sequences which cannot be distinsguished at resolution ${r_n}$ , and get a distance on the resulting quotient. For this, we fix once and for all a non principal ultrafilter ${\omega}$ . This is a finitely additive measure on subsets of ${{\mathbb N}}$ which takes only values ${0}$ and ${1}$ , and is ${0}$ on all finite sets. Using the axiom of choice, one can show that such things exist.

Proposition 3 Let ${Z}$ be a compact Hausdorff space, ${(z_n)}$ a sequence of points of ${Z}$ . Then there is a unique point ${z_{\infty}\in Z}$ such that for all neighborhoods ${U}$ of ${z_{\infty}}$ , ${\omega(\{n\,;\, z_n \in U\})=1}$ . This is denoted by

$\displaystyle \begin{array}{rcl} z_{\infty}:=\lim_{\omega}z_n . \end{array}$

Based on this fact, for any two sequences ${\hat{x}=(x_n)}$ , ${\hat{y}=(y_n)}$ belonging to ${\hat{X}}$ , the limit ${d_{\omega}(\hat{x},\hat{y})=\lim_{\omega}\frac{1}{r_n}d(x_n ,y_n)}$ exists and defines a pseudo metric on ${\hat{X}}$ .

Definition 4 Let ${\omega}$ be a non principal ultrafilter on ${{\mathbb N}}$ . The ${\omega}$ -asymptotic cone of ${X}$ is

$\displaystyle \begin{array}{rcl} X_{\omega}:=(\hat{X},d_{\omega})/\sim \end{array}$

where two sequences are identified iff their ${d_{\omega}}$ vanishes.

Theorem 5 (Gromov) Let ${X}$ be a geodesic metric space. Then ${X}$ is hyperbolic iff all its asymptotic cones are metric trees.

In fact, one can do with a fix ultrafilter, and all sequences ${r_n}$ , ${p_n}$ , or the sequence ${r_n =1/n}$ , and all sequences ${p_n}$ and ultrafilters ${\omega}$ .

1.2. Lipschitz maps to asymptotic cones

Proposition 6 (Wenger 2008) Let ${X}$ be a geodesic metric space, ${Y}$ a geodesic thickening with quadratic filling function. If ${X}$ is not hyperbolic, there exists an asymptotic cone ${X_{\omega}}$ of ${X}$ , a compact set ${K\subset {\mathbb R}^2}$ and a Lipschitz map ${\psi:K \rightarrow X_{\omega}}$ such that ${\psi(K)}$ has positive ${2}$ -dimensional Hausdorff measure.

Definition 7 Say that a metric space ${Z}$ is purely ${2}$ -unrectifiable if all images of Lipschitz maps from subsets of ${R^2}$ to ${Z}$ have zero ${2}$ -dimensional Hausdorff measure.

Example 1 The first Heisenberg group ${H^1}$ (and its quaternionic and octonionic analogues) have purely ${2}$ -unrectifiable asymptotic cones.

More generally, this holds for Carnot groups whose first layer of the stratification of the Lie algebra does not contain any ${2}$ -dimensional sub-algebra.

We shall not prove this. This depends on Rademacher’s a.e. differentiability theorem.

Corollary 8 Let ${X}$ be geodesic and not hyperbolic. Assume that all asymptotic cones of ${X}$ are purely ${2}$ -unrectifiable. Then for all geodesic thickenings ${Y}$ of ${X}$ ,

$\displaystyle \begin{array}{rcl} \lim_{r\rightarrow\infty}\frac{FA_0^{X,Y}(r)}{r^2}=+\infty. \end{array}$

1.3. Metric differentiability

Definition 9 Let ${U}$ be an open subset of ${{\mathbb R}^n}$ . Let ${\psi:U\rightarrow X}$ be Lipschitz. The metric directional derivative of ${\psi}$ in direction ${v\in{\mathbb R}^n}$ is

$\displaystyle \begin{array}{rcl} md_{z}\psi(v):=\lim_{r\rightarrow 0}\frac{d(\psi(z+rv),\psi(z))}{|r|}. \end{array}$

Theorem 10 (Kirchheim 1994) For a.e. ${z\in U}$ , metric derivatives at ${z}$ exist in all directions. Moreover, there exist a countable family of disjoint compact sets filling almost all of ${U}$ such that on each such compact set ${K}$ , for all ${\epsilon>0}$ there exists ${r(K,\epsilon)>0}$ such that for all ${z\in K}$ , ${z_i \in K\cap B(z,r(K,\epsilon))}$ ,

$\displaystyle \begin{array}{rcl} |d(\psi(z_1),\psi(z_2))-md_{z}\psi(z_1 -z_2)|\leq\epsilon|z_1 -z_2|. \end{array}$

The estimate in Theorem implies that ${md_z \psi}$ is a semi-norm. When it is a norm, then ${\psi:(K,md_z \psi)\rightarrow X}$ is nearly isometric around ${z}$ ( ${1+\delta}$ -bilipschitz in a small enough ball).

Remark 1 Theorem 1 extends to the case where ${U}$ is merely a Borel set.

One merely needs to extend ${\psi}$ to a neighborhood, with values in ${L_{\infty}(X)}$ .

Proof: (Sketch). Existence of ${md_z \psi}$ .

Step 1: Case ${n=1}$ .

Let ${x_n}$ be a dense countable subset of ${\psi({\mathbb R})}$ . Then ${\gamma_n (t)=d(x_n ,\psi(t))}$ is Lipschitz ${{\mathbb R}\rightarrow{\mathbb R}}$ so a.e. differentiable. Set

$\displaystyle \begin{array}{rcl} a(t):=\sup_n |\dot{\gamma}_n (t)|. \end{array}$

Then

$\displaystyle \begin{array}{rcl} \liminf_{r\rightarrow 0}\frac{d(\psi(t+r), \psi(t))}{|r|} \geq \liminf_{r\rightarrow 0}\frac{|\gamma_n (t+r) - \gamma_n (t)|}{|r|}= |\dot{\gamma}_n (t)|. \end{array}$

Furthermore, for any ${t}$ , ${s}$ ,

$\displaystyle \begin{array}{rcl} d(\psi(t),\psi(s))&=&\sup_{n}|\gamma_n (t)-\gamma(s)|\\ &\leq& \sup_{n}\int_{s}^{t}|\dot{\gamma}_n (\tau)|\,d\tau\\ &\leq&\int_{s}^{t}a(\tau)\,d\tau. \end{array}$

At a Lebesgue point ${t}$ of continuity of ${a}$ , this integral converges to ${a(t)}$ , and

$\displaystyle \begin{array}{rcl} \limsup_{r\rightarrow 0}\frac{d(\psi(t+r),\psi(t))}{|r|}\leq\limsup|\frac{1}{r}\int_{t}^{t+r}a(\tau)\,d\tau| = a(t). \end{array}$

Step 2: There exists ${md_z \psi}$ for a.e. ${z}$ and all ${v}$ .

Step 1 gives it for a dense countable set of vectors. Triangle inequality implies it for all ${v}$ .

Step 3: Prove estimate on ${|d(\psi(z_1),\psi(z_2))-md_{z}\psi(z_1 -z_2)|}$ .

Write

$\displaystyle \begin{array}{rcl} |d(\psi(z+v),\psi(z+w))-md_{z}\psi(v-w)|&\leq& |d(\psi(z+v),\psi(z+w))-md_{z+w}\psi(v-w)|\\ &&+|md_{z}\psi(v-w)-md_{z}\psi(v-w)|. \end{array}$

By Lusin’s theorem, partition into compact subsets on which ${z\mapsto md_z \psi}$ , ${K\rightarrow C(S^{n-1})}$ , is continuous and on which, by Egorov’s theorem,

$\displaystyle \begin{array}{rcl} \frac{d(\psi(z+rv),\psi(z))}{|r|} \end{array}$

converges uniformly to ${md_z \psi(v)}$ , and this does the job. $\Box$

I wrote a slightly simplified proof of Theorem 1 as an appendix of my paper on Characterization of real trees...

1.4. Area formula

Theorem 11 (Kirchheim 1994) Let ${U}$ be an open subset of ${{\mathbb R}^n}$ . Let ${\psi:U\rightarrow X}$ be Lipschitz. Let ${A\subset{\mathbb R}^n}$ be Lebesgue measurable. Then

$\displaystyle \begin{array}{rcl} \int_{X}N(\psi_{|A},x)\,d\mathcal{H}^{n}(x)=\int_{A}J_n (md_z \psi)\,d\mathcal{H}^n (z). \end{array}$

Here, for a semi-norm ${s}$ on ${{\mathbb R}^n}$ , define ${J_n (s)=0}$ unless ${s}$ is a norm, in which case ${J_n (s)}$ is the ${n}$ -dimensional Hausdorff measure, in the Banach space ${({\mathbb R}^n ,s)}$ , on the unit cube.

Note that one recovers our definition of area for Lipschitz maps of the ${2}$ -disk.

Proof: Step 1: Show that the image by ${\psi}$ of the set of points where ${md_z \psi}$ is not defined or nor a norm has vanishing ${h}$ -Hausdorff measure.

Step 2: Use the fact that ${\psi}$ is nearly isometric on the pieces of a partition. $\Box$

2. Proof of sharp gap theorem

2.1. Sketch of the proof

By contradiction. Assume ${X}$ has nearly Euclidean filling function, but is not hyperbolic. Then there exists an asymptotic cone ${X_{\omega}}$ and a Lipschitz map ${\psi:K\rightarrow X_{\omega}}$ with ${\mathcal{H}^2 (\psi(K))>0}$ .

By Kirchheim’s theorems 1 and 11, after possibly replacing ${K}$ by a smaller set, there exists a Lebesgue density point ${z}$ at which the metric derivative exists and is a norm, and ${\psi:(K,md_z \psi)\rightarrow X_{\omega}}$ is nearly isometric around ${z}$ , i.e. ${(1+\delta)}$ -bilipschitz in a small enough ball.

Let ${I}$ be a convex isoperimetric set in ${({\mathbb R}^2, md_z \psi)}$ . By convex geometry, the isoperimetric profile of a ${2}$ -dimensional Banach space is minimal for Euclidean plane, so

$\displaystyle \begin{array}{rcl} \mathcal{H}^2 (I)\geq \frac{1}{4\pi}\mathrm{length}(\partial I). \end{array}$

Let ${\gamma:S^1 \rightarrow \partial I}$ be an arc-length parametrization. Choose ${k\geq 2}$ large enough (depending on ${\epsilon}$ and ${\delta}$ ) and cut ${\partial I}$ in ${k}$ equidistant intervals, leading to vertex set ${\Lambda}$ . By assumption, there exist arbitrarily large ${r_1}$ such that ${X_1 :=(X,\frac{1}{r_1}d_X)}$ contains a nearly isometric copy of ${(\Lambda,\,md_z \psi)}$ . Connect these vertices by geodesics to get a piecewise geodesic loop ${c}$ in ${X_1}$ . By assumption, there exists a Lipschitz extension ${\phi:D^2 \rightarrow L_{\infty}(X_1)}$ of ${c}$ of area

$\displaystyle \begin{array}{rcl} \mathrm{Area}(\phi)\leq \frac{1-\epsilon}{4\pi}\mathrm{length}(c)^2 \sim \frac{1-\varepsilon}{4\pi}length(\partial I)^2 . \end{array}$

One would like to extend the ${(1+\delta)}$ -Lipschitz map ${\psi^{-1}}$ to a map from ${L_\infty(X_1)}$ to ${V}$ in order to push the filling ${\phi}$ to ${V}$ .

Not possible without increasing Lipschitz constant by a factor of ${\sqrt{2}}$ . Instead, view ${V=({\mathbb R}^2, md_z \psi)}$ as a linear subspace of ${\ell_{\infty}}$ . Use injectivity of ${L_{\infty}}$ to extend into a ${(1+\delta)}$ -Lipschitz map

$\displaystyle \begin{array}{rcl} \eta:L_{\infty}(X_1)\rightarrow \ell_{\infty}. \end{array}$

Then ${\eta\circ\phi:D^2 \rightarrow \ell_{\infty}}$ nearly fills ${\gamma}$ . Adding little ${2}$ -dimensional pieces, one gets ${\bar{\gamma}:D^2 \rightarrow\ell_{\infty}}$ with ${\bar{\gamma}_{|S^1}=\gamma}$ and

$\displaystyle \begin{array}{rcl} \mathrm{Area}(\bar{\gamma})\leq (1+...)\mathrm{length}(\gamma)^2 <\frac{1}{4\pi}\mathrm{length}(\partial I)^2 . \end{array}$

Open question (Busemann): Let ${W\subset E}$ be an affine subspace of a Banach space ${E}$ , let ${\Omega\subset W}$ be a convex compact subset. Does ${\Omega}$ minimize ${2}$ -dimensional Hausdorff measure among all Lipschitz disks in ${E}$ with same boundary ?

Answer unknown. Fortunately, we can remedy this. Take the Holmes-Thompson area ${\mu_{HT}}$ . instead of Hausdorff measure. It has the following properties.

${\mu_{HT}\leq \mathcal{H}^2}$ .
${\mu_{HT}(I)=\frac{1}{4\pi}\mathrm{length}(\partial I)^2}$ .
Affine disks minimize ${\mu_{HT}}$ (Dima Burago and Sergey Ivanov 2002).

Therefore we have found in ${\ell_{\infty}}$ a filling ${\eta\circ\phi}$ of ${\partial I}$ with

$\displaystyle \begin{array}{rcl} \mu_{HT}(\eta\circ\phi)<\frac{1}{4\pi}\mathrm{length}(\partial I)^2 , \end{array}$

contradicting above three properties. This completes the proof.

Remark 2 Properties 2. and 3. is easy for Gromov’s ${mass^*}$ -measure.

If we choose the ${mass^*}$ notion of area in the definition of the filling function ${FA_0^{X,\infty}(r)}$ , we do not need to resort to Burago-Ivanov’s result. We can then also allow surfaces of arbitrary genus as fillings in the function ${FA_0^{X,\infty}(r)}$ making it potentially smaller than when only allowing disk fillings and thus making the assumption 2. in the gap theorem even weaker.

2.2. Proof of Proposition 6

We shall prove a stronger statement that will be needed again for nilpotent groups. We need some preparation. To motivate it, let us attempt to prove

Proposition 12 (Wenger 2008) Let ${X}$ be a geodesic metric space, ${Y}$ a geodesic thickening with quadratic filling. If ${X}$ is not hyperbolic, there exists an asymptotic cone ${X_{\omega}}$ of ${X}$ , a compact set ${K\subset {\mathbb R}^2}$ and a Lipschitz map ${\psi:K \rightarrow X_{\omega}}$ such that ${\psi(K)}$ has positive ${2}$ -dimensional Hausdorff measure.

By Gromov’s hyperbolicity criterion, there exists an asymptotic cone ${X_{\omega}}$ which is not a tree, i.e. contains a non trivial loop. One obtains from it a sequence of uniformy Lipschitz loops ${\gamma_n}$ in ${(X,\frac{1}{n}d}$ . Fill ${\gamma_n}$ with a Lipschitz disk ${\Sigma_n}$ . Will ${\Sigma_n}$ (sub)-converge to a disk in ${X_{\omega}}$ ?

Related problem: Plateau’s problem in ${{\mathbb R}^3}$ . Try to solve it by the direct method, i.e. pick a minimizing sequence of disks (now ${\gamma_n}$ is always the same curve). There could be thin spikes of small area sticking out, so no convergence. People have used the following tricks:

Douglas and Rado minimize Dirichlet integral instead. Scope limited to ${2}$ -disks.
Federer and Fleming introduce normal and integral currents, i.e. linear functionals generalizing surfaces. They show that minimizing sequences have subsequences which converge to limit functionals which have nice structure.

2.3. Euclidean theory of currents

Idea: Every ${m}$ -dimensional oriented submanifold with boundary of ${{\mathbb R}^n}$ defines a linear functional on compactly supported differential ${m}$ -forms, with the following properties.

Stokes’ theorem: ${N(d\omega)=\partial N(\omega)}$ .
Duality volume/ ${L_{\infty}}$ -norm: $\displaystyle \mathrm{Volume}(N)=\sup\{N(\omega)\,;\,\|\omega\|_{\infty}\leq 1\}.$

So define currents are elements of the dual space ${M_m}$ to the space of compactly supported ${m}$ -forms normed by ${L_{\infty}}$ -norm.

Banach-Alaoglu’s theorem gives that the unit ball in ${M_m}$ , i.e. currents of mass ${\leq 1}$ , is weak ${*}$ -sequentially compact.

We want to define integral currents as the closure in ${M_m}$ of oriented submanifolds with boundary. Consider the following family of currents:

$\displaystyle \begin{array}{rcl} T(\omega)=\int_{\Sigma}\Theta\langle \omega,\tau \rangle\,d\mathcal{H}^{m}, \end{array}$

where ${\Sigma}$ is countably ${\mathcal{H}^{m}}$ -rectifiable. ${\Theta\in L_1 (\Sigma,{\mathbb Z})}$ is a density, ${\tau}$ is an ${m}$ -vector defining an orientation on the (a.e. defined) tangent space of ${\Sigma}$ .

Definition 13 An integral current is a current ${T}$ such that both ${T}$ and ${\partial T}$ are of the above form.

Theorem 14 (Closure theorem). If a sequence of integral currents with bounded mass and bounded boundary mass converges in ${M_m}$ , then the limit is an integral current.

2.4. Metric theory of currents

Idea (de Giorgi): Replace smooth differential form ${\omega=f\,d\pi_1 \wedge \cdots \wedge d\pi_m}$ with ${m+1}$ -tuple of Lipschitz functions ${(f,\pi_1 ,\ldots,\pi_m)}$ .

The formula

$\displaystyle \begin{array}{rcl} d(f\,d\pi_1 \wedge \cdots \wedge d\pi_m)=df\wedge d\pi_1 \wedge \cdots \wedge d\pi_m \end{array}$

suggests generalization

$\displaystyle \begin{array}{rcl} \partial T (f,\pi_1 ,\ldots,\pi_m)=T(1,f,\pi_1 ,\ldots,\pi_m). \end{array}$

This leads to a solid theory. Here is our generalized Proposition 12.

Theorem 15 (Wenger) Let ${X}$ be a geodesic metric space, ${Y}$ a geodesic thickening with quadratic filling. Assume that

$\displaystyle \begin{array}{rcl} FA_0^{X,Y}(r)\preceq r^2 . \end{array}$

Every asymptotic cone of ${X}$ has quadratic isoperimetric inequality for integral ${1}$ -currents.

Cornulier: Is there a converse ? Answer: Gromov, using his coarse filling, proves that quadratic filling in all cones implies ${r^{2+\epsilon}}$ -filling in ${X}$ .

4 Responses to Notes of Stefan Wenger’s lecture nr 2

Stefan Wenger says:

March 3, 2011 at 14:09

As written, the last sentence of Section 2.1 is a bit misleading. It would be more accurate to write:

If we choose the mass* notion of area in the definition of the filling function FA_0^{X,\infty}(r) we do not need to resort to Burago-Ivanov’s result. We can then also allow surfaces of arbitrary genus as fillings in the function FA_0^{X,\infty}(r) making it potentially smaller than when only allowing disk fillings and thus making the assumption 2. in the gap theorem even weaker.

metric2011 says:

March 3, 2011 at 22:53

Dear Stefan,

Thanks for your comment. I edited the file as you suggested.
Can you please have a look at the notes of your first lecture ? The statement of Gromov’s thickening lemma, to be found at the end, looks suspicious to me. I tend to believe that the thickening improves the filling function for small values of r and should not change it for larger values of r. So it cannot state that FA^{X,Y}(r)\preceq r^2 for all r.

Sincerely,

- Stefan Wenger says:
  
  March 4, 2011 at 11:26
  
  Dear Pierre,
  
  Thanks for making the changes. I will look at all of lecture 1 and also lecture 2 today and will write again.
  
  As for the proposition about thickenings: yes, the thickening improves the filling function to quadratic on small scale (r<1) and has growth on the large scale bounded by that of Gromov's coarse isoperimetric function. One can even find a thickening Y such that FA_0^Y has growth at most that of Gromov's coarse function at large scales and such that FA_0^Y(r) is bounded by Cr^2 for 0<r<1, where C is a suitable constant. Note that FA_0^{X,Y} is bounded by FA_0^Y so this is even a bit better than what you wrote in the notes now. We will need this somewhat better statement when trying to produce uniformly compact fillings of given curves in lecture 3. The proof of the proposition (which is not so difficult) can be found in my paper on the sharp isoperimetric constant. I was unaware of a proof by Gromov. Is it the one you told about in the Filling Riemannian Manifolds paper?
  
Stefan Wenger says:

March 5, 2011 at 00:39

Dear Pierre,

Thank you for taking notes. Here are, as promised, some minor corrections to the notes of lecture 2.

– Paragraph after Theorem 1: it should read “provided the coarse filling function has at most quadratic growth.”
– In Section 1.1, after Proposition 3: in the definition d_\omega(\hat{x}, \hat{y}) insert \lim_\omega
– In Section 1.1, after Theorem 5: write r_n instead of r-n
– In Section 1.2, Proposition 6: “geodesic thickening with quadratic filling function”
– In Section 1.2, in Definition 7: complete the sentence as follows: “… if all images of Lipschitz maps from subsets of R^2 to Z have zero 2-dimensional Hausdorff measure.”
– In Section 1.2, after Example 1: “… for Carnot groups whose first layer of the stratification of the Lie algebra does not contain any 2-dimensional sub-algebra.”
– In Section 1.3, Proof of Theorem 10:
– In step 1, the first inequality should read $$\liminf_{r\to0}\frac{d(\psi(t+r), \psi(t))}{|r|} \geq \liminf_{r\to0}\frac{|\gamma_n(t+r) – \gamma_n(t)|}{|r|}= |\dot{\gamma}_n(t)|.$$
– In the equation that follows, the term “\sup_n\int_s^t|\dot{\gamma}_n(\tau)|d\tau” should be between inequality signs
– In the equation that follows, at the very end insert “| = a(t)”
– In step 3, in the equation, replace w by v-w at the end of the first line
– In Section 2.1, end of second line in first paragraph: H^2(\psi(K))>0
– In Section, 2.1, middle of proof:
– in the equation, replace $\sim length(\partial I)$ by $\sim \frac{1-\varepsilon}{4\pi}length(\partial I)^2.$
– on the next line, complete the sentence “One would like to” to “One would like to extend the (1+\delta)-Lipschitz map \psi^{-1} to a map from L_\infty(X_1) to V in order to push the filling \phi to V.”
– In Section 2.1, in the equation before the Open question, replace the first occurrence of \gamma by \bar{\gamma}
– Section 2.2, title: “Proof of Proposition 6”, not Proposition 14

Thank you again. With kind regards,
Stefan

	metric2011 on Notes of Sa’ar Hersonsky…
	CH on Videos
	Stefan Wenger on Notes of Stefan Wenger’s…
	Stefan Wenger on Notes of Stefan Wenger’s…
	Stefan Wenger on Notes of Stefan Wenger’s…