Notes of Viktor Schroeder’s second informal Cambridge lecture 23-05-2017

Posted on May 23, 2017 by metric2011

Moebius structures on boundaries, II

1. Ptolemaic Moebius structures

Recall that a Moebius structure is Ptolemaic if cross-ratios satisfy the Ptolemaic inequality,

\displaystyle \begin{array}{rcl} \rho_{12}\rho_{34}\leq \rho_{23}\rho_{14}+\rho_{13}\rho_{24}. \end{array}

This means that {crt} takes its values in the triangle {\Delta\subset\hat\Sigma} with vertices at the extra points {(1:1:0),(1:0:1),(0:1:1)}.

Examples

  1. Boundaries of {CAT(-1)}-spaces, in their Bourdon metric, are Ptolemaic.
  2. Boundaries of hyperbolic groups admit natural Ptolemaic Moebius structures. This follows from a construction by Mineyev-Yu, as observed by Nica. Furthermore, Nica-Spakula observed that visual metrics associated to Green metrics associated to random walks also define Prolemaic Moebius structures.

There is an indirect link between Ptolemaic and triangle inequalities.

  • Given a bounded Ptolemaic Moebius structure, pick a point {\omega\in X} and form the semi-metric {\rho_\omega} which sends {\omega} at infinity. Then {\rho_\omega} is a metric.
  • Two metrics in the Moebius class which send the same point to infinity are proportional.
  • A Ptolemaic Moebius structure always contains at least one bounded metric. Indeed, given any bounded semi-metric in the structure, add an ideal point {\hat X=X\cup\{\hat\omega\}} et extend {\rho} by {\hat\rho(x,\hat\omega)=\rho(x,o)+1}, where {o} is an arbitrary origin in {X}. Then {\hat\rho_{\hat\omega}} is a bounded metric in the Moebius structure of {X}.

2. The space of metrics of a Moebius structure

Given two Moebius-equivalent metrics {\rho} and {\tau}, there exists a Lipschitz function {\lambda} such that

\displaystyle \begin{array}{rcl} \rho(x,y)=\lambda(x)\lambda(y)\tau(x,y). \end{array}

One denotes by

\displaystyle \begin{array}{rcl} \lambda=(\frac{d\rho}{d\tau})^{1/2}. \end{array}

Question. Is every Moebius space the boundary of some space in a natural sense ?

This space should be the space {\mathcal{M}} of metrics in the Moebius structure. The map

\displaystyle \begin{array}{rcl} \rho\mapsto -\log\frac{d\rho}{d\tau}(x) \end{array}

can be viewed as a Busemann function on {\mathcal{M}}. It is well defined up to an additive constant, since at each point,

\displaystyle \begin{array}{rcl} \frac{d\rho}{d\tau}\frac{d\tau}{d\sigma}=\frac{d\rho}{d\sigma}. \end{array}

Kingshook Biswas defines {\mathcal{M}_a} as the subset of diameter 1, antipodal metrics in the Moebius structure. Antipodal means that every point has an other point lying at distance 1 from it. Then Biswas embeds {\mathcal{M}_a} into {C^0(X)} by {\rho\mapsto -\log\frac{d\rho}{d\tau}}. The image is a closed subset, {\mathcal{M}_a} inherits a proper metric (balls are compact) that does not depend on the choice of reference metric {\tau}. He shows that, in the case of the boundary of a {CAT(-1)} space {Y}, {Y} isometrically embeds in {\mathcal{M}_a}, which is within bounded Hausdorff distance from {Y}.

3. Hausdorff measure

Assume that {D} is the Haudorff dimension of {(X,\rho)}. Then Hausdorff measures corresponding to different metrics in the Moebius structures differ by a factor

\displaystyle \begin{array}{rcl} \frac{d\mu_\rho}{d\mu_\tau}(x)=(\frac{d\rho}{d\tau}(x))^D. \end{array}

Therefore the measure on pairs

\displaystyle \begin{array}{rcl} d\nu(x,y)=\rho(y,s)^{-2D}d\mu_\rho(x)d\mu_\rho(y) \end{array}

is invariant on {X\times X}.

Cross-ratio define a kind of distance on pairs.

4. Methods

4.1. Spheres between points

Given distinct points {p,q,y\in X}, the sets {\{x\in X\,;\,[x:y:p:q]=1\}} form a 1-parameter family of “spheres” separating {p} from {q}. Indeed, by the cocycle condition, this is an equivalence relation.

4.2. Jorgensen’s inequality

I learned this from J. Parker and S. Markham. Given a loxodromic transformation {\alpha\in Moeb(X)}, with axis {p,q}, set

\displaystyle \begin{array}{rcl} a= \rho(p,q)\rho(z,\alpha z),\quad b=\rho(z,p)\rho(\alpha z,q),\quad c=\rho(\alpha z,p)\rho(z,q). \end{array}

Then {\frac{a}{b},\frac{b}{c},\frac{c}{a}} are cross-ratios. Define

\displaystyle \begin{array}{rcl} m_\alpha=\sup_z \frac{a}{b}\frac{a}{c}. \end{array}

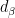
Proposition 1 Let {X} be a compact Moebius space. let {\Gamma} be a discrete group of Moebius transformations of {X}. Then for every loxodromic elements {\alpha,\beta\in\Gamma}, {d_\alpha} and {d_\beta}

\displaystyle \begin{array}{rcl} m_\alpha^2(d((p,q),(\beta p,\beta q))+1)\geq 1. \end{array}

5. Next time

I will explain Beyrer’s Moebius structure on the Furstenberg boundary of higher rank symmetric spaces.

About metric2011

metric2011 is a program of Centre Emile Borel, an activity of Institut Henri Poincaré, 11 rue Pierre et Marie Curie, 75005 Paris, France. See http://www.math.ens.fr/metric2011/
This entry was posted in seminar and tagged . Bookmark the permalink.

Leave a comment